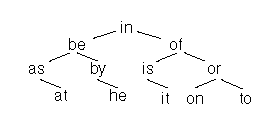반응형
3-웨이 트리인 TST의 구현과 TST의 기본적인 성능향상방법에 대해서 알아본다.
Ternary Search Tree
데이터를 저장할 때 많이 사용되는 것을 꼽으라면 java.util.Hashtable 이나 java.util.HashMap일 것이다. 이 둘은 해시테이블을 구현한 것으로서 키값을 사용하여 객체를 저장하고 읽을 수 있을 뿐만 아니라 알고리즘의 성능은 O(1)이다. 따라서 이 두 클래스를 사용하면 키값을 사용하여 매우 빠르게 해시테이블에 데이터를 저장하거나 해시테이블로부터 데이터를 읽어올 수 있다.
하지만, 해시테이블은 정렬 상태로 데이터를 유지하지 않기 때문에, 데이터의 집합을 정렬된 상태로 유지해야 하는 경우에는 사용할 수 없다는 단점이 있다. 이러한 경우에 사용되는 것이 바로 트리이다. 트리를 사용하면 비교적 손쉽게 데이터를 정렬된 상태로 저장할 수 있게 된다.
우리가 흔히 사용하는 DBMS 역시 데이터를 정렬된 상태로 저장하기 트리를 사용하며(물론 DBMS에서 사용되는 트리는 복잡한 구조를 갖고 있다.), 일반적인 프로그램에서도 트리를 사용해야 하는 경우가 발생한다. 흔히 사용되는 트리로는 바이너리 트리와 트라이가 있다. 이 두 트리는 비교적 구현이 쉬우면서도 알맞은 성능을 제공한다. 바이너리 트리의 공간 사용의 장점과 트라이의 검색 속도의 장점을 합한 것이 바로 TST(Ternary Search Tree)이다.
TST는 문자열을 정렬하고 검색하는 데 있어서 매우 빠른 속도를 낸다. 또한, TST를 이용할 경우 부분적으로 일치하는 문자열의 집합도 쉽게 구할 수 있다. 이 글에서는 TST의 구조와 구현에 대해서 알아보며, TST의 성능을 향상시킬 수 있는 몇 가지 방안에 대해서 알아본다.
TST의 구조
TST의 구조에 대해서 알아보기 위해 간단하게 단어 12개를 사용하여 바이너리 트리와 디지탈 서치 트라이 그리고 TST가 어떤 모양을 나타내는지 살펴보자. 여기서 사용할 단어는 다음과 같다.
이 12개의 단어를 사용하여 균형을 이룬 바이너리 트리를 구성한다면 다음 그림과 같을 것이다.
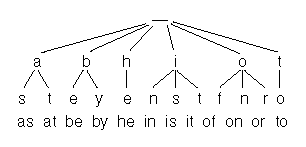
이제 디지탈 서치 트라이를 살펴보자. 트라이의 경우 다음과 같은 구조를 이룰 것이다.
디지털 서치 트라이는 위 그림에서 볼 수 있듯이 문자열을 글자 단위로 저장한다. 이러한 특징 때문에, 디지털 서치 트라이의 검색 속도는 같은 길이를 갖는 단어의 경우 거의 같으며, 평균적으로 바이너리 서치 트리에 비해 매우 빠른 검색 속도를 제공한다. 하지만, 디지털 서치 트라이는 메모리를 많이 차지하는 단점이 있다. 위 그림에서는 표시하지 않았지만, 만약 이 트리가 알파벳만을 저장한다고 할 경우 각 노드는 26개의 가지(branch)를 갖게 된다. (물론 소문자만 저장한다고 가정할 때 그렇다. 대문자까지 저장할 경우 두배인 52개의 하위 트리를 사용하게 된다.) 즉, 사용되는 단어가 적을 경우 그 만큼 아무값도 갖지 않는 노드의 개수가 증가하는 것이다.
이제 바이너리 트리와 디지털 서치 트라이의 장점을 취합한 TST의 구조를 살펴보자. TST의 구조는 다음 그림과 같다.
TST의 각 노드는 세 개의 서브 트리를 갖고 있으며, 왼쪽 서브 트리는 작은 값을, 가운데 서브 트리는 같은 값을, 그리고 오른쪽 서브 트리는 큰값을 갖도록 구성되어 있다. 예를 들어, 위 그림에서 "he"를 검색한다고 해 보자. 'h'는 루트 노드의 값인 'i'보다 작으므로 왼쪽 서브 트리를 검색한다. 그 다음으로 'h'는 'b' 보다 크므로 'b' 값을 갖는 노드의 오른쪽 서브 트리를 검색한다. 'b'의 오른쪽 서브 트리에 있는 노드의 값이 'h' 이므로 가운데 서브 트리를 검색하며, 마지막으로 검색할 노드의 값이 'e' 이므로 검색을 완료한다. 검색 과정은 바이너리 트리와 비슷하지만 각 노드마다 완전한 문자열이 아닌 하나의 문자를 나타낸다는 점은 디지털 서치 트라이와 비슷하다. 또한, 디지털 서치 트라이와 달리 불필요하게 낭비되는 노드를 갖고 있지 않다는 점에서는 바이너리 트리와 비슷하다. 종합적으로 정리하면, TST는 바이너리 트리의 공간 효율과 디지털 서치 트라이의 빠른 검색 속도의 장점을 합쳐놓은 트리라고 할 수 있다.
TST의 구현
TST의 구현은 그렇게 어렵지 않다. 이전에 C/C++ 또는 자바를 사용하여 링크트 리스트나 트리를 구현해 본 사람이라면 손쉽게 구현할 수 있다. TST는 RecursiveTST 클래스와 RecursiveTSTNode 클래스로 구성된다. RecursiveTSTNode 클래스만으로도 구현할 수 있지만, 여기서는 역할을 분리한다는 의미에서 이 두 클래스를 사용하였다. RecursiveTST 클래스는 트리 자체를 나타내며, RecursiveTSTNode 클래스는 트리에 있는 각각의 노드를 나타낸다.
먼저 RecursiveTST 클래스의 소스 코드를 살펴보자.
위 코드를 보면 RecursiveTST 클래스는 RecursiveTSTNode 타입의 root 필드와 트리에 객체를 삽입하고 트리에서 객체를 읽어올 때 사용되는 get() 메소드와 put() 메소드로 구성되어 있다는 것을 알 수 있다. 이 두 메소드는 내부적으로 RecursiveTSTNode 클래스의 static() 메소드인 search()와 insert() 메소드를 사용한다.
RecursiveTSTNode 클래스가 실제로 필요한 것들을 구현하고 있다. TST는 세 개의 가지를 갖고 있기 때문에, RecursiveTSTNode 클래스는 각각의 서브 트리를 나타내기 위해서 3개의 RecursiveTSTNode 타입인 high, equal, low 필드를 갖고 있으며, 그 노드가 나타내는 글자를 저장하기 위해 char 타입인 splitChar 필드를 갖고 있다. 그리고 실제 그 노드가 나타내는 값을 저장하기 위해 Object 타입인 value 필드를 갖고 있다. RecursiveTSTNode 클래스의 개략적인 코드는 다음과 같다.
이제, search() 메소드를 살펴보자. search() 메소드는 다음과 같이 구현된다.
search() 메소드에서 첫번째 파라미터 p는 검색을 시작할 노드를 나타내며, 두번째 파라미터 key는 검색할 키값을 나타낸다. 그리고 마지막 파라미터인 index는 키값에 있는 글자중 현재 노드(즉, 첫번째 파라미터로 전달받은 p)와 관련된 단어인 splitChar와 비교할 글자의 인덱스를 나타낸다. 현재 노드가 갖고 있는 글자와 키값에서 인덱스가 index인 글자를 비교하여 현재 노드의 값이 작을 경우 p.low가 나타내는 서브 트리부터 검색을 시작하고, 반대로 클 경우에는 p.high가 나타내는 서브 트리부터 검색을 시작한다. (재귀 호출을 사용하고 있다!)
만약 현재 노드의 단어와 키값의 단어가 같다면, 키값의 가장 마지막 단어와 비교한 것인지 판단한다. 그래서 가장 마지막 단어라면 현재 노드가 저장하고 있는 값(p.value)를 리턴하고 그렇지 않다면 p.equal이 나타내는 서브 트리부터 검색을 시작한다. 여기서 주목할 점은 현재 노드의 단어와 키값의 비교 단어가 같은 경우에만 재귀 호출을 할 때 index 값에 1을 더한다는 사실이다.
이제 TST에 값을 삽입할 때 사용되는 insert() 메소드를 살펴보자.
insert() 메소드는 search() 메소드와 크게 다르지 않다. 파라미터로 전달받는 p, key, index는 search() 메소드에서의 파라미터와 같은 의미를 가지며, 네번째 파라미터인 value는 노드에 저장될 값을 나타낸다. insert() 메소드에서는 트리를 생성하기 때문에, 검색할 노드가 null인 경우 새로운 노드를 생성한다.
RecursiveTST 클래스를 사용하는 방법은 매우 간단하다. 다음과 같이 먼저 RecursiveTST 클래스의 인스턴스를 생성한 후, get()과 put() 메소드를 사용하여 필요에 따라 데이터를 TST에 넣거나 TST로부터 읽어오면 된다.
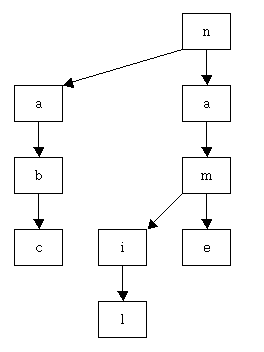
실제로 위와 같이 "name", "nail", "abc"를 키 값으로 사용할 경우 다음과 같은 TST가 생성된다.
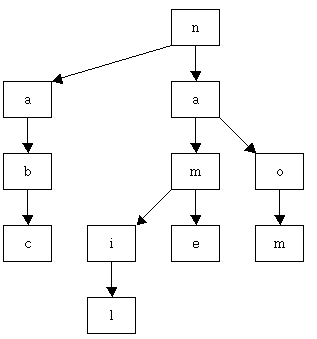
위 그림에서 각 상자 안에 있는 글자는 그 노드가 나타내는 글자(즉, RecursiveTSTNode의 splitChar 필드의 값)를 나타낸다. 그리고 왼쪽으로 뻗은 화살표와 가운데로 뻗은 화살표는 각각 RecursiveTSTNode의 low 필드와 equal 필드를 나타낸다. 이 상태에서 TST에 키값이 "nom"인 객체를 추가할 경우(즉, tree.put("nom", value)를 수행할 경우) 위 그림에 표시된 TST는 다음과 같이 변경될 것이다.
get()과 put()을 사용하여 TST를 사용하는 것을 보면 RecursiveTST를 Hashtable이나 HashMap의 트리 형태로 생각할 수도 있다. 이렇게 생각할 경우 이미 자바2에서 제공하고 있는 HashTree가 있는 데 궂이 RecursiveTST를 사용하여 또 다른 형태의 트리를 구현했는 지 의아해 할지도 모른다. 하지만, TST를 사용할 경우 바이너리 트리와 같은 단순한 트리로는 할 수 없는 문자열의 부분 일치와 같은 문자열 처리 기능을 구현할 수 있다. 이에 대한 내용은 이 글의 2부에서 살펴보기로 한다.
TST의 성능향상
앞에서 작성한 RecursiveTSTNode는 매우 간단하게 TST를 구현하고 있다. 하지만, RecursiveTSTNode 클래스를 실제로 사용하기에는 성능이 문제가 될 수 있다. 따라서 실제로 이 클래스를 어플리케이션에서 사용하기 위해서는 성능 향상을 위한 튜닝 작업이 필요하다. 이 글의 나머지 부분에서는 성능이 향상된 TST를 구현하는 것에 대해서 알아보도록 하자.
스텝1 - String 대신 char 배열을 사용한다.
가장 손쉽게 성능을 향상시킬 수 있는 부분은 문자열과 관련된 부분이다. RecursiveTSTNode 클래스의 search() 메소드와 insert() 메소드를 살펴보면 키값이 포함하고 있는 각 글자를 현재 노드의 글자와 비교하기 위해서 String의 charAt() 메소드를 사용하는 것을 알 수 있다. 하지만, String을 char 배열로 변환한 후, 그 배열을 사용하여 비교할 경우 메소드 호출에 따른 시간 낭비를 줄일 수 있다.
스텝2 - 재귀 호출 메소드를 반복적(iterative) 형태로 변경한다.
두번째로 변경할 부분은 재귀 호출 부분이다. 재귀 호출은 코드를 매우 간단하고 이해하기 쉽게 만들어주는 장점이 있으나, 재귀 호출은 계속된 메소드 호출과 스택의 사용에 따른 성능 저하를 일으키는 원인이 될 수도 있다. 재귀 호출을 for 구문이나 while 구문을 사용하여 반복적인(iterative) 형태로 변경하는 것이 쉬운 것은 아니지만, 다행히도 RecursiveTSTNode의 insert() 메소드와 search() 메소드를 반복적 형태로 변경하는 것은 그리 어렵지 않다.
이제 RecursiveTST 클래스와 RecursiveTSTNode 클래스에 스텝1과 스텝2를 적용하여 성능을 향상한 IterativeTST 클래스와 IterativeTSTNode 클래스의 소스 코드를 살펴보자. 코드 자체가 복잡한 편이 아니므로 별다른 설명은 하지 않겠다. 먼저 IterativeTST 클래스의 소스 코드는 다음과 같다.
위 코드를 키 값으로 전달받은 String 객체를 char 배열로 변환한 후, char 배열을 IterativeTSTNode 클래스의 search() 메소드와 insert() 메소드에 전달하는 것을 알 수 있다. RecursiveTST 클래스와 차이점이 있다면, put() 메소드에서 루트 노드를 직접 생성한다는 점이다. RecursiveTST 클래스의 put() 메소드는 루트 노드를 직접 생성하지 않으며, 루트 노드를 포함한 모든 노드의 생성은 RecursiveTSTNode 클래스의 insert() 메소드에서 이루어졌다.
이제 IterativeTSTNode 클래스를 살펴보자. IterativeTSTNode 클래스의 소스 코드는 다음과 같다.
스텝1과 스텝2를 적용한 IterativeTSTNode 클래스는 실제로 RecursiveTSTNode 클래스에서 비해 25-30% 정도 성능이 향상된다.
스텝3 - 오브젝트 풀의 사용
세번째 단계에 적용할 수 있는 방법은 미리 사용가능한 노드 객체를 생성해 놓는 것이다. 이는 데이터베이스 커넥션 풀링이나 쓰레드 풀링과 같은 개념으로 보면 된다. 실제로 TST를 창안한 Bentley와 Sedgewick 역시 TST의 성능 향상을 극대화하기 위해 미리 메모리를 할당하는 방법을 언급하고 있다. 최종적으로 오브젝트 풀 기능을 추가한 TSTree 클래스와 TSTreeNode 클래스를 작성해보자. 참고로 최종 단계의 TST 구현 버전은 TSTree 클래스에 TSTreeNode 클래스를 이너 클래스로 정의하였다.
오브젝트 풀과 관련된 메소드는 오브젝트 풀을 생성해주는 createPool() 메소드와 오브젝트 풀로부터 새로운 노드를 리턴해주는 newNode() 메소드이다. 먼저 createPool() 메소드를 살펴보자.
createPool() 메소드는 생성할 풀의 개수를 입력받고 그 개수만큼 TSTreeNode 객체를 생성한다. 풀은 링크트 리스트 구조를 갖도록 만들어진다. 이제 풀로부터 이미 생성되어 있는 TSTreeNode 객체를 구해주는 newNode() 메소드를 살펴보자.
newNode() 메소드는 단순히 풀의 가장 앞에 있는 객체를 리턴해준다. 풀을 사용하기 위해서는 TSTreeNode 클래스의 생성자 대신에 newNode() 메소드를 호출해주면 된다. 다음은 완전한 TSTreeNode 클래스의 소스 코드이다.
오브젝트 풀을 사용하면 전체 성능이 처음에 작성한 RecursiveTST에 비해 35-60% 정도 향상된다. 35%에서 60%에 이르기까지 성능 향상 정도가 차이가 나는 것은 TST에 삽입하는 데이터의 정렬 정도에 따라서 TST의 생성된 모양이 달라지기 때문이다.
여기서 성능을 좀 더 향상시키기 위해서는 트리를 포인터 형태가 아닌 배열 형태로 유지하는 것이다. 이 방법이 어렵지는 않지만, 소스 코드가 복잡해지므로 여기서는 생략하기로 한다. 이에 대해 알고 싶은 사람은 Oreilly의 'Java Performance Tuning' 책을 참고하기 바란다.
결론
1부에서는 TST가 무엇이며, 어떤 구조로 이루어져 있는지에 대해서 알아봤으며, 실제 구현과 성능을 향상시키는 방법에 대해서 알아보았다. 2부에서는 TST를 응용하여 문자열의 부분 일치를 어떻게 처리할 수 있는 지에 대해 알아보며, 실제 TST를 어떻게 활용할 수 있는지에 대해서 알아볼 것이다.
관련링크:
Ternary Search Tree
데이터를 저장할 때 많이 사용되는 것을 꼽으라면 java.util.Hashtable 이나 java.util.HashMap일 것이다. 이 둘은 해시테이블을 구현한 것으로서 키값을 사용하여 객체를 저장하고 읽을 수 있을 뿐만 아니라 알고리즘의 성능은 O(1)이다. 따라서 이 두 클래스를 사용하면 키값을 사용하여 매우 빠르게 해시테이블에 데이터를 저장하거나 해시테이블로부터 데이터를 읽어올 수 있다.
하지만, 해시테이블은 정렬 상태로 데이터를 유지하지 않기 때문에, 데이터의 집합을 정렬된 상태로 유지해야 하는 경우에는 사용할 수 없다는 단점이 있다. 이러한 경우에 사용되는 것이 바로 트리이다. 트리를 사용하면 비교적 손쉽게 데이터를 정렬된 상태로 저장할 수 있게 된다.
우리가 흔히 사용하는 DBMS 역시 데이터를 정렬된 상태로 저장하기 트리를 사용하며(물론 DBMS에서 사용되는 트리는 복잡한 구조를 갖고 있다.), 일반적인 프로그램에서도 트리를 사용해야 하는 경우가 발생한다. 흔히 사용되는 트리로는 바이너리 트리와 트라이가 있다. 이 두 트리는 비교적 구현이 쉬우면서도 알맞은 성능을 제공한다. 바이너리 트리의 공간 사용의 장점과 트라이의 검색 속도의 장점을 합한 것이 바로 TST(Ternary Search Tree)이다.
TST는 문자열을 정렬하고 검색하는 데 있어서 매우 빠른 속도를 낸다. 또한, TST를 이용할 경우 부분적으로 일치하는 문자열의 집합도 쉽게 구할 수 있다. 이 글에서는 TST의 구조와 구현에 대해서 알아보며, TST의 성능을 향상시킬 수 있는 몇 가지 방안에 대해서 알아본다.
TST의 구조
TST의 구조에 대해서 알아보기 위해 간단하게 단어 12개를 사용하여 바이너리 트리와 디지탈 서치 트라이 그리고 TST가 어떤 모양을 나타내는지 살펴보자. 여기서 사용할 단어는 다음과 같다.
as, at, be, by, he, in, is, it, of, on, or, to
이 12개의 단어를 사용하여 균형을 이룬 바이너리 트리를 구성한다면 다음 그림과 같을 것이다.
이제 디지탈 서치 트라이를 살펴보자. 트라이의 경우 다음과 같은 구조를 이룰 것이다.
디지털 서치 트라이는 위 그림에서 볼 수 있듯이 문자열을 글자 단위로 저장한다. 이러한 특징 때문에, 디지털 서치 트라이의 검색 속도는 같은 길이를 갖는 단어의 경우 거의 같으며, 평균적으로 바이너리 서치 트리에 비해 매우 빠른 검색 속도를 제공한다. 하지만, 디지털 서치 트라이는 메모리를 많이 차지하는 단점이 있다. 위 그림에서는 표시하지 않았지만, 만약 이 트리가 알파벳만을 저장한다고 할 경우 각 노드는 26개의 가지(branch)를 갖게 된다. (물론 소문자만 저장한다고 가정할 때 그렇다. 대문자까지 저장할 경우 두배인 52개의 하위 트리를 사용하게 된다.) 즉, 사용되는 단어가 적을 경우 그 만큼 아무값도 갖지 않는 노드의 개수가 증가하는 것이다.
이제 바이너리 트리와 디지털 서치 트라이의 장점을 취합한 TST의 구조를 살펴보자. TST의 구조는 다음 그림과 같다.
TST의 각 노드는 세 개의 서브 트리를 갖고 있으며, 왼쪽 서브 트리는 작은 값을, 가운데 서브 트리는 같은 값을, 그리고 오른쪽 서브 트리는 큰값을 갖도록 구성되어 있다. 예를 들어, 위 그림에서 "he"를 검색한다고 해 보자. 'h'는 루트 노드의 값인 'i'보다 작으므로 왼쪽 서브 트리를 검색한다. 그 다음으로 'h'는 'b' 보다 크므로 'b' 값을 갖는 노드의 오른쪽 서브 트리를 검색한다. 'b'의 오른쪽 서브 트리에 있는 노드의 값이 'h' 이므로 가운데 서브 트리를 검색하며, 마지막으로 검색할 노드의 값이 'e' 이므로 검색을 완료한다. 검색 과정은 바이너리 트리와 비슷하지만 각 노드마다 완전한 문자열이 아닌 하나의 문자를 나타낸다는 점은 디지털 서치 트라이와 비슷하다. 또한, 디지털 서치 트라이와 달리 불필요하게 낭비되는 노드를 갖고 있지 않다는 점에서는 바이너리 트리와 비슷하다. 종합적으로 정리하면, TST는 바이너리 트리의 공간 효율과 디지털 서치 트라이의 빠른 검색 속도의 장점을 합쳐놓은 트리라고 할 수 있다.
TST의 구현
TST의 구현은 그렇게 어렵지 않다. 이전에 C/C++ 또는 자바를 사용하여 링크트 리스트나 트리를 구현해 본 사람이라면 손쉽게 구현할 수 있다. TST는 RecursiveTST 클래스와 RecursiveTSTNode 클래스로 구성된다. RecursiveTSTNode 클래스만으로도 구현할 수 있지만, 여기서는 역할을 분리한다는 의미에서 이 두 클래스를 사용하였다. RecursiveTST 클래스는 트리 자체를 나타내며, RecursiveTSTNode 클래스는 트리에 있는 각각의 노드를 나타낸다.
먼저 RecursiveTST 클래스의 소스 코드를 살펴보자.
public class RecursiveTST {
private RecursiveTSTNode root;
public Object get(String key) {
return RecursiveTSTNode.search(root, key, 0);
}
public void put(String key, Object value) {
root = RecursiveTSTNode.insert(root, key, 0, value);
}
}
private RecursiveTSTNode root;
public Object get(String key) {
return RecursiveTSTNode.search(root, key, 0);
}
public void put(String key, Object value) {
root = RecursiveTSTNode.insert(root, key, 0, value);
}
}
위 코드를 보면 RecursiveTST 클래스는 RecursiveTSTNode 타입의 root 필드와 트리에 객체를 삽입하고 트리에서 객체를 읽어올 때 사용되는 get() 메소드와 put() 메소드로 구성되어 있다는 것을 알 수 있다. 이 두 메소드는 내부적으로 RecursiveTSTNode 클래스의 static() 메소드인 search()와 insert() 메소드를 사용한다.
RecursiveTSTNode 클래스가 실제로 필요한 것들을 구현하고 있다. TST는 세 개의 가지를 갖고 있기 때문에, RecursiveTSTNode 클래스는 각각의 서브 트리를 나타내기 위해서 3개의 RecursiveTSTNode 타입인 high, equal, low 필드를 갖고 있으며, 그 노드가 나타내는 글자를 저장하기 위해 char 타입인 splitChar 필드를 갖고 있다. 그리고 실제 그 노드가 나타내는 값을 저장하기 위해 Object 타입인 value 필드를 갖고 있다. RecursiveTSTNode 클래스의 개략적인 코드는 다음과 같다.
public class RecursiveTSTNode {
char splitChar;
RecursiveTSTNode low;
RecursiveTSTNode equal;
RecursiveTSTNode high;
Object value;
public static Object search(RecursiveTSTNode p, String key, int index) {
// TST로부터 특정 키값에 해당하는 노드가 저장하고 있는 값을 읽어온다.
.....
}
public static RecursiveTSTNode insert(RecursiveTSTNode p, String key, int index, Object value) {
// TST의 키값 key에 해당하는 노드에 value를 값으로 저장한다.
.....
}
public RecursiveTSTNode(char c) {
splitChar = c;
}
}
char splitChar;
RecursiveTSTNode low;
RecursiveTSTNode equal;
RecursiveTSTNode high;
Object value;
public static Object search(RecursiveTSTNode p, String key, int index) {
// TST로부터 특정 키값에 해당하는 노드가 저장하고 있는 값을 읽어온다.
.....
}
public static RecursiveTSTNode insert(RecursiveTSTNode p, String key, int index, Object value) {
// TST의 키값 key에 해당하는 노드에 value를 값으로 저장한다.
.....
}
public RecursiveTSTNode(char c) {
splitChar = c;
}
}
이제, search() 메소드를 살펴보자. search() 메소드는 다음과 같이 구현된다.
public static Object search(RecursiveTSTNode p, String key, int index) {
char c;
// 만약 노드가 없을 경우(null일 경우)
if (p == null) return null;
// str의 index에 있는 글자가 현재 노드에 있는 글자보다
// 작은 값을 갖는 경우
else if ( (c = key.charAt(index)) < p.splitChar )
return search(p.low, key, index);
// str의 index에 있는 글자가 현재 노드에 있는 글자보다
// 큰 값을 갖는 경우
else if ( c > p.splitChar)
return search(p.high, key, index);
// str의 index에 있는 글자와 현재 노드에 있는 글자가
// 같은 값을 갖는 경우
else {
if (index == (key.length() -1) )
return p.value;
else
return search(p.equal, key, index+1);
}
}
char c;
// 만약 노드가 없을 경우(null일 경우)
if (p == null) return null;
// str의 index에 있는 글자가 현재 노드에 있는 글자보다
// 작은 값을 갖는 경우
else if ( (c = key.charAt(index)) < p.splitChar )
return search(p.low, key, index);
// str의 index에 있는 글자가 현재 노드에 있는 글자보다
// 큰 값을 갖는 경우
else if ( c > p.splitChar)
return search(p.high, key, index);
// str의 index에 있는 글자와 현재 노드에 있는 글자가
// 같은 값을 갖는 경우
else {
if (index == (key.length() -1) )
return p.value;
else
return search(p.equal, key, index+1);
}
}
search() 메소드에서 첫번째 파라미터 p는 검색을 시작할 노드를 나타내며, 두번째 파라미터 key는 검색할 키값을 나타낸다. 그리고 마지막 파라미터인 index는 키값에 있는 글자중 현재 노드(즉, 첫번째 파라미터로 전달받은 p)와 관련된 단어인 splitChar와 비교할 글자의 인덱스를 나타낸다. 현재 노드가 갖고 있는 글자와 키값에서 인덱스가 index인 글자를 비교하여 현재 노드의 값이 작을 경우 p.low가 나타내는 서브 트리부터 검색을 시작하고, 반대로 클 경우에는 p.high가 나타내는 서브 트리부터 검색을 시작한다. (재귀 호출을 사용하고 있다!)
만약 현재 노드의 단어와 키값의 단어가 같다면, 키값의 가장 마지막 단어와 비교한 것인지 판단한다. 그래서 가장 마지막 단어라면 현재 노드가 저장하고 있는 값(p.value)를 리턴하고 그렇지 않다면 p.equal이 나타내는 서브 트리부터 검색을 시작한다. 여기서 주목할 점은 현재 노드의 단어와 키값의 비교 단어가 같은 경우에만 재귀 호출을 할 때 index 값에 1을 더한다는 사실이다.
이제 TST에 값을 삽입할 때 사용되는 insert() 메소드를 살펴보자.
public static RecursiveTSTNode insert(RecursiveTSTNode p, String key, int index, Object value) {
char c;
if (p == null) p = new RecursiveTSTNode(key.charAt(index));
if ( (c = key.charAt(index)) < p.splitChar)
p.low = insert(p.low, key, index, value);
else if (c == p.splitChar) {
if (index == (key.length() - 1) )
p.value = value;
else
p.equal = insert(p.equal, key, index+1, value);
} else
p.high = insert(p.high, key, index, value);
return p;
}
char c;
if (p == null) p = new RecursiveTSTNode(key.charAt(index));
if ( (c = key.charAt(index)) < p.splitChar)
p.low = insert(p.low, key, index, value);
else if (c == p.splitChar) {
if (index == (key.length() - 1) )
p.value = value;
else
p.equal = insert(p.equal, key, index+1, value);
} else
p.high = insert(p.high, key, index, value);
return p;
}
insert() 메소드는 search() 메소드와 크게 다르지 않다. 파라미터로 전달받는 p, key, index는 search() 메소드에서의 파라미터와 같은 의미를 가지며, 네번째 파라미터인 value는 노드에 저장될 값을 나타낸다. insert() 메소드에서는 트리를 생성하기 때문에, 검색할 노드가 null인 경우 새로운 노드를 생성한다.
RecursiveTST 클래스를 사용하는 방법은 매우 간단하다. 다음과 같이 먼저 RecursiveTST 클래스의 인스턴스를 생성한 후, get()과 put() 메소드를 사용하여 필요에 따라 데이터를 TST에 넣거나 TST로부터 읽어오면 된다.
RecursiveTST tree = new RecursiveTST();
tree.put("name", "이름");
tree.put("nail", "손톱");
tree.put("abc", "알파벳");
// get
tree.get("name") );
tree.get("abc") );
tree.get("memo");
tree.put("name", "이름");
tree.put("nail", "손톱");
tree.put("abc", "알파벳");
// get
tree.get("name") );
tree.get("abc") );
tree.get("memo");
실제로 위와 같이 "name", "nail", "abc"를 키 값으로 사용할 경우 다음과 같은 TST가 생성된다.
위 그림에서 각 상자 안에 있는 글자는 그 노드가 나타내는 글자(즉, RecursiveTSTNode의 splitChar 필드의 값)를 나타낸다. 그리고 왼쪽으로 뻗은 화살표와 가운데로 뻗은 화살표는 각각 RecursiveTSTNode의 low 필드와 equal 필드를 나타낸다. 이 상태에서 TST에 키값이 "nom"인 객체를 추가할 경우(즉, tree.put("nom", value)를 수행할 경우) 위 그림에 표시된 TST는 다음과 같이 변경될 것이다.
get()과 put()을 사용하여 TST를 사용하는 것을 보면 RecursiveTST를 Hashtable이나 HashMap의 트리 형태로 생각할 수도 있다. 이렇게 생각할 경우 이미 자바2에서 제공하고 있는 HashTree가 있는 데 궂이 RecursiveTST를 사용하여 또 다른 형태의 트리를 구현했는 지 의아해 할지도 모른다. 하지만, TST를 사용할 경우 바이너리 트리와 같은 단순한 트리로는 할 수 없는 문자열의 부분 일치와 같은 문자열 처리 기능을 구현할 수 있다. 이에 대한 내용은 이 글의 2부에서 살펴보기로 한다.
TST의 성능향상
앞에서 작성한 RecursiveTSTNode는 매우 간단하게 TST를 구현하고 있다. 하지만, RecursiveTSTNode 클래스를 실제로 사용하기에는 성능이 문제가 될 수 있다. 따라서 실제로 이 클래스를 어플리케이션에서 사용하기 위해서는 성능 향상을 위한 튜닝 작업이 필요하다. 이 글의 나머지 부분에서는 성능이 향상된 TST를 구현하는 것에 대해서 알아보도록 하자.
스텝1 - String 대신 char 배열을 사용한다.
가장 손쉽게 성능을 향상시킬 수 있는 부분은 문자열과 관련된 부분이다. RecursiveTSTNode 클래스의 search() 메소드와 insert() 메소드를 살펴보면 키값이 포함하고 있는 각 글자를 현재 노드의 글자와 비교하기 위해서 String의 charAt() 메소드를 사용하는 것을 알 수 있다. 하지만, String을 char 배열로 변환한 후, 그 배열을 사용하여 비교할 경우 메소드 호출에 따른 시간 낭비를 줄일 수 있다.
스텝2 - 재귀 호출 메소드를 반복적(iterative) 형태로 변경한다.
두번째로 변경할 부분은 재귀 호출 부분이다. 재귀 호출은 코드를 매우 간단하고 이해하기 쉽게 만들어주는 장점이 있으나, 재귀 호출은 계속된 메소드 호출과 스택의 사용에 따른 성능 저하를 일으키는 원인이 될 수도 있다. 재귀 호출을 for 구문이나 while 구문을 사용하여 반복적인(iterative) 형태로 변경하는 것이 쉬운 것은 아니지만, 다행히도 RecursiveTSTNode의 insert() 메소드와 search() 메소드를 반복적 형태로 변경하는 것은 그리 어렵지 않다.
이제 RecursiveTST 클래스와 RecursiveTSTNode 클래스에 스텝1과 스텝2를 적용하여 성능을 향상한 IterativeTST 클래스와 IterativeTSTNode 클래스의 소스 코드를 살펴보자. 코드 자체가 복잡한 편이 아니므로 별다른 설명은 하지 않겠다. 먼저 IterativeTST 클래스의 소스 코드는 다음과 같다.
public class IterativeTST {
private IterativeTSTNode root;
private char keyArr[] = new char[100]; // 키 값의 길이는 100자까지 허용한다.
public Object get(String key) {
if (root == null) return null;
key.getChars(0, key.length(), keyArr, 0);
return root.search(keyArr, 0, key.length() - 1);
}
public Object put(String key, Object value) {
key.getChars(0, key.length(), keyArr, 0);
if (root == null) root = new IterativeTSTNode(keyArr[0]);
return root.insert(keyArr, 0, key.length() - 1, value);
}
}
private IterativeTSTNode root;
private char keyArr[] = new char[100]; // 키 값의 길이는 100자까지 허용한다.
public Object get(String key) {
if (root == null) return null;
key.getChars(0, key.length(), keyArr, 0);
return root.search(keyArr, 0, key.length() - 1);
}
public Object put(String key, Object value) {
key.getChars(0, key.length(), keyArr, 0);
if (root == null) root = new IterativeTSTNode(keyArr[0]);
return root.insert(keyArr, 0, key.length() - 1, value);
}
}
위 코드를 키 값으로 전달받은 String 객체를 char 배열로 변환한 후, char 배열을 IterativeTSTNode 클래스의 search() 메소드와 insert() 메소드에 전달하는 것을 알 수 있다. RecursiveTST 클래스와 차이점이 있다면, put() 메소드에서 루트 노드를 직접 생성한다는 점이다. RecursiveTST 클래스의 put() 메소드는 루트 노드를 직접 생성하지 않으며, 루트 노드를 포함한 모든 노드의 생성은 RecursiveTSTNode 클래스의 insert() 메소드에서 이루어졌다.
이제 IterativeTSTNode 클래스를 살펴보자. IterativeTSTNode 클래스의 소스 코드는 다음과 같다.
public class IterativeTSTNode {
char splitChar;
IterativeTSTNode low;
IterativeTSTNode equal;
IterativeTSTNode high;
Object value;
public Object search(char key[], int index, int lastIndex) {
char c;
for (IterativeTSTNode node = this ; node != null ; ) {
if ( (c = key[index]) < node.splitChar)
node = node.low;
else if ( c == node.splitChar) {
if (index == lastIndex)
return node.value;
index++;
node = node.equal;
} else
node = node.high;
}
return null;
}
public Object insert(char key[], int index, int lastIndex, Object value) {
IterativeTSTNode node = this;
char c;
while(true) {
if ( (c = key[index]) < node.splitChar ) {
if (node.low == null)
node.low = new IterativeTSTNode(c);
node = node.low;
} else if ( c == node.splitChar ) {
if (index == lastIndex) {
Object old = node.value;
node.value = value;
return old;
}
index ++;
c = key[index];
if (node.equal == null)
node.equal = new IterativeTSTNode(c);
node = node.equal;
} else {
if (node.high == null)
node.high = new IterativeTSTNode(c);
node = node.high;
}
}
}
public IterativeTSTNode(char c) {
splitChar = c;
}
}
char splitChar;
IterativeTSTNode low;
IterativeTSTNode equal;
IterativeTSTNode high;
Object value;
public Object search(char key[], int index, int lastIndex) {
char c;
for (IterativeTSTNode node = this ; node != null ; ) {
if ( (c = key[index]) < node.splitChar)
node = node.low;
else if ( c == node.splitChar) {
if (index == lastIndex)
return node.value;
index++;
node = node.equal;
} else
node = node.high;
}
return null;
}
public Object insert(char key[], int index, int lastIndex, Object value) {
IterativeTSTNode node = this;
char c;
while(true) {
if ( (c = key[index]) < node.splitChar ) {
if (node.low == null)
node.low = new IterativeTSTNode(c);
node = node.low;
} else if ( c == node.splitChar ) {
if (index == lastIndex) {
Object old = node.value;
node.value = value;
return old;
}
index ++;
c = key[index];
if (node.equal == null)
node.equal = new IterativeTSTNode(c);
node = node.equal;
} else {
if (node.high == null)
node.high = new IterativeTSTNode(c);
node = node.high;
}
}
}
public IterativeTSTNode(char c) {
splitChar = c;
}
}
스텝1과 스텝2를 적용한 IterativeTSTNode 클래스는 실제로 RecursiveTSTNode 클래스에서 비해 25-30% 정도 성능이 향상된다.
스텝3 - 오브젝트 풀의 사용
세번째 단계에 적용할 수 있는 방법은 미리 사용가능한 노드 객체를 생성해 놓는 것이다. 이는 데이터베이스 커넥션 풀링이나 쓰레드 풀링과 같은 개념으로 보면 된다. 실제로 TST를 창안한 Bentley와 Sedgewick 역시 TST의 성능 향상을 극대화하기 위해 미리 메모리를 할당하는 방법을 언급하고 있다. 최종적으로 오브젝트 풀 기능을 추가한 TSTree 클래스와 TSTreeNode 클래스를 작성해보자. 참고로 최종 단계의 TST 구현 버전은 TSTree 클래스에 TSTreeNode 클래스를 이너 클래스로 정의하였다.
오브젝트 풀과 관련된 메소드는 오브젝트 풀을 생성해주는 createPool() 메소드와 오브젝트 풀로부터 새로운 노드를 리턴해주는 newNode() 메소드이다. 먼저 createPool() 메소드를 살펴보자.
private void createPool(int poolSize) {
TSTreeNode temp;
for (int i = poolSize ; i > 0 ; i-- ) {
temp = pool;
pool = new TSTreeNode(' ');
pool.equal = temp;
}
}
TSTreeNode temp;
for (int i = poolSize ; i > 0 ; i-- ) {
temp = pool;
pool = new TSTreeNode(' ');
pool.equal = temp;
}
}
createPool() 메소드는 생성할 풀의 개수를 입력받고 그 개수만큼 TSTreeNode 객체를 생성한다. 풀은 링크트 리스트 구조를 갖도록 만들어진다. 이제 풀로부터 이미 생성되어 있는 TSTreeNode 객체를 구해주는 newNode() 메소드를 살펴보자.
// 풀에서 하나의 노드를 읽어온다.
private TSTreeNode newNode(char c) {
if (remain == 0) {
return new TSTreeNode(c);
}
TSTreeNode ret = pool;
pool = pool.equal; // 풀에 있는 다음 객체를 가리킴.
ret.equal = ret.high = ret.low = null;
ret.splitChar = c;
remain--; // 풀에 남아 있는 객체의 개수 1 감소.
return ret;
}
private TSTreeNode newNode(char c) {
if (remain == 0) {
return new TSTreeNode(c);
}
TSTreeNode ret = pool;
pool = pool.equal; // 풀에 있는 다음 객체를 가리킴.
ret.equal = ret.high = ret.low = null;
ret.splitChar = c;
remain--; // 풀에 남아 있는 객체의 개수 1 감소.
return ret;
}
newNode() 메소드는 단순히 풀의 가장 앞에 있는 객체를 리턴해준다. 풀을 사용하기 위해서는 TSTreeNode 클래스의 생성자 대신에 newNode() 메소드를 호출해주면 된다. 다음은 완전한 TSTreeNode 클래스의 소스 코드이다.
public class TSTree {
private TSTreeNode root;
private char keyArr[] = new char[100]; // 키 값의 길이는 100자까지 허용한다.
private TSTreeNode pool; // 풀에서 현재 위치를 가리킨다.
private int remain; // 현재 풀에 남아 있는 노드의 개수
public TSTree(int poolSize) {
createPool(poolSize);
remain = poolSize;
}
private void createPool(int poolSize) {
TSTreeNode temp;
for (int i = poolSize ; i > 0 ; i-- ) {
temp = pool;
pool = new TSTreeNode(' ');
pool.equal = temp;
}
}
// 풀에서 하나의 노드를 읽어온다.
private TSTreeNode newNode(char c) {
if (remain == 0) {
return new TSTreeNode(c);
}
TSTreeNode ret = pool;
pool = pool.equal; // 풀에 있는 다음 객체를 가리킴.
ret.equal = ret.high = ret.low = null;
ret.splitChar = c;
remain--; // 풀에 남아 있는 객체의 개수 1 감소.
return ret;
}
public Object get(String key) {
if (root == null) return null;
key.getChars(0, key.length(), keyArr, 0);
return root.search(keyArr, 0, key.length() - 1);
}
public Object put(String key, Object value) {
key.getChars(0, key.length(), keyArr, 0);
if (root == null) root = newNode(keyArr[0]);
return root.insert(keyArr, 0, key.length() - 1, value);
}
class TSTreeNode {
char splitChar;
TSTreeNode low;
TSTreeNode equal;
TSTreeNode high;
Object value;
public Object search(char key[], int index, int lastIndex) {
char c;
for (TSTreeNode node = this ; node != null ; ) {
if ( (c = key[index]) < node.splitChar)
node = node.low;
else if ( c == node.splitChar) {
if (index == lastIndex)
return node.value;
index++;
node = node.equal;
} else
node = node.high;
}
return null;
}
public Object insert(char key[], int index, int lastIndex, Object value) {
TSTreeNode node = this;
char c;
while(true) {
if ( (c = key[index]) < node.splitChar ) {
if (node.low == null)
node.low = newNode(c);
node = node.low;
} else if ( c == node.splitChar ) {
if (index == lastIndex) {
Object old = node.value;
node.value = value;
return old;
}
index ++;
c = key[index];
if (node.equal == null)
node.equal = newNode(c);
node = node.equal;
} else {
if (node.high == null)
node.high = newNode(c);
node = node.high;
}
}
}
public TSTreeNode(char c) {
splitChar = c;
}
}
}
private TSTreeNode root;
private char keyArr[] = new char[100]; // 키 값의 길이는 100자까지 허용한다.
private TSTreeNode pool; // 풀에서 현재 위치를 가리킨다.
private int remain; // 현재 풀에 남아 있는 노드의 개수
public TSTree(int poolSize) {
createPool(poolSize);
remain = poolSize;
}
private void createPool(int poolSize) {
TSTreeNode temp;
for (int i = poolSize ; i > 0 ; i-- ) {
temp = pool;
pool = new TSTreeNode(' ');
pool.equal = temp;
}
}
// 풀에서 하나의 노드를 읽어온다.
private TSTreeNode newNode(char c) {
if (remain == 0) {
return new TSTreeNode(c);
}
TSTreeNode ret = pool;
pool = pool.equal; // 풀에 있는 다음 객체를 가리킴.
ret.equal = ret.high = ret.low = null;
ret.splitChar = c;
remain--; // 풀에 남아 있는 객체의 개수 1 감소.
return ret;
}
public Object get(String key) {
if (root == null) return null;
key.getChars(0, key.length(), keyArr, 0);
return root.search(keyArr, 0, key.length() - 1);
}
public Object put(String key, Object value) {
key.getChars(0, key.length(), keyArr, 0);
if (root == null) root = newNode(keyArr[0]);
return root.insert(keyArr, 0, key.length() - 1, value);
}
class TSTreeNode {
char splitChar;
TSTreeNode low;
TSTreeNode equal;
TSTreeNode high;
Object value;
public Object search(char key[], int index, int lastIndex) {
char c;
for (TSTreeNode node = this ; node != null ; ) {
if ( (c = key[index]) < node.splitChar)
node = node.low;
else if ( c == node.splitChar) {
if (index == lastIndex)
return node.value;
index++;
node = node.equal;
} else
node = node.high;
}
return null;
}
public Object insert(char key[], int index, int lastIndex, Object value) {
TSTreeNode node = this;
char c;
while(true) {
if ( (c = key[index]) < node.splitChar ) {
if (node.low == null)
node.low = newNode(c);
node = node.low;
} else if ( c == node.splitChar ) {
if (index == lastIndex) {
Object old = node.value;
node.value = value;
return old;
}
index ++;
c = key[index];
if (node.equal == null)
node.equal = newNode(c);
node = node.equal;
} else {
if (node.high == null)
node.high = newNode(c);
node = node.high;
}
}
}
public TSTreeNode(char c) {
splitChar = c;
}
}
}
오브젝트 풀을 사용하면 전체 성능이 처음에 작성한 RecursiveTST에 비해 35-60% 정도 향상된다. 35%에서 60%에 이르기까지 성능 향상 정도가 차이가 나는 것은 TST에 삽입하는 데이터의 정렬 정도에 따라서 TST의 생성된 모양이 달라지기 때문이다.
여기서 성능을 좀 더 향상시키기 위해서는 트리를 포인터 형태가 아닌 배열 형태로 유지하는 것이다. 이 방법이 어렵지는 않지만, 소스 코드가 복잡해지므로 여기서는 생략하기로 한다. 이에 대해 알고 싶은 사람은 Oreilly의 'Java Performance Tuning' 책을 참고하기 바란다.
결론
1부에서는 TST가 무엇이며, 어떤 구조로 이루어져 있는지에 대해서 알아봤으며, 실제 구현과 성능을 향상시키는 방법에 대해서 알아보았다. 2부에서는 TST를 응용하여 문자열의 부분 일치를 어떻게 처리할 수 있는 지에 대해 알아보며, 실제 TST를 어떻게 활용할 수 있는지에 대해서 알아볼 것이다.
관련링크: